Físicos mexicanos resuelven un problema milenario

Un trío de físicos de la UNAM y del Tec de Monterrey han resuelto un problema de la óptica, con más de 2000 años de antiguedad (el problema Wasserman-Wolf). En su artículo, publicado en la revista Applied Optics, Rafael González-Acuña, Héctor Chaparro-Romo y Julio Gutiérrez-Vega describen las matemáticas necesarias para resolver el problema, aportan algunos ejemplos de posibles aplicaciones y describen la eficiencia de sus resultados, con base en algunas relevantes pruebas de su propio modelo.

El propio Isaac Newton no lo pudo resolver en su momento y aunque ya se habían encontrado aproximaciones, nadie había encontrado la respuesta completa.

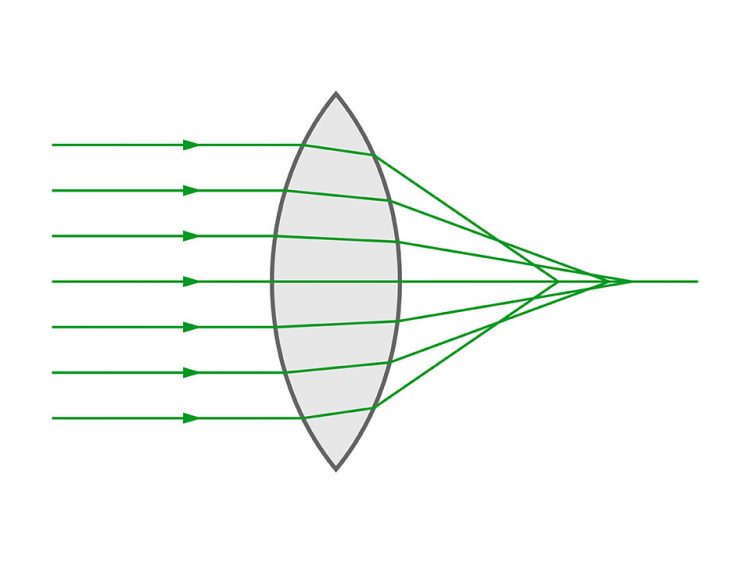
Se trata de la solución a la aberración esférica en lentes ópticos, con la que ahora muchas industrias (telescopios, cámaras, etc.)  podrán reducir grandes costos.

Una mañana, luego de meses y meses de intentar solucionar la ecuación que planteaba el problema, Rafael González supo que ya lo tenía.

El propio egresado del Tec en Ingeniería Física Industrial narra la experiencia: “Subí a mi cuarto, me puse a programar, vi que salió y me puse a brincar de emoción”.

Alejandro Chaparro, egresado de la UNAM, había invitado a Rafael a solucionar el problema; él  llevaba ya 3 años buscando resolverlo. Ambos se conocieron en la maestría en el Centro de Investigaciones de Óptica.

“Me acuerdo que una mañana me estaba preparando un pan con Nutella, y de repente dije: ¡madres! ¡está ahí! “.- Rafael González-Acuña

“Sabía que era un problema mítico. Ahí conocí a Alejandro; me insistía y me invitaba a que resolviéramos el problema. Yo le decía que era un pantano y no iba a poder”, afirma Rafael.

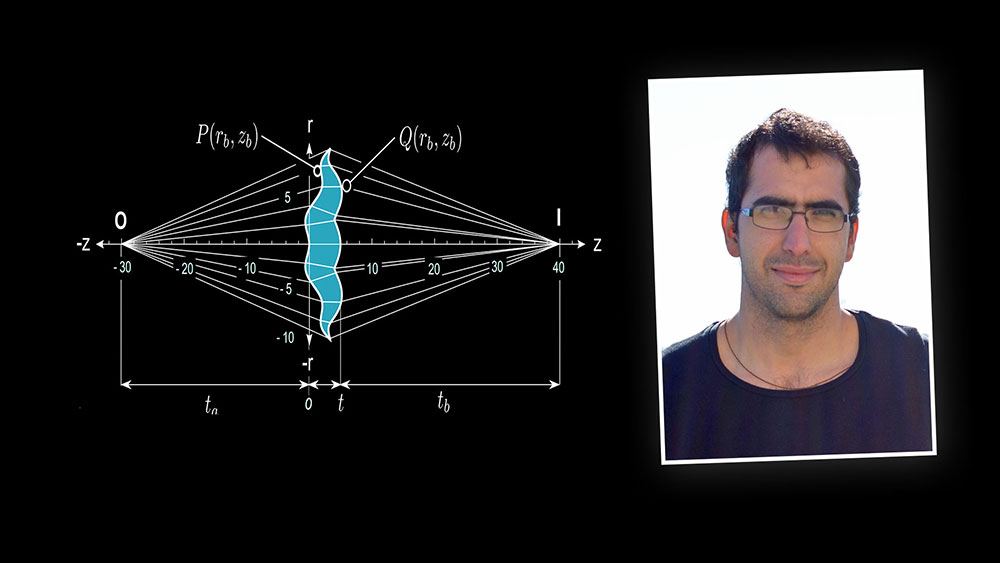
Un problema milenario

El primero en fundamentar el problema fue el matemático griego Diocles, hace más de 2 mil años. Después, durante siglos, científicos como Newton o Leibniz habían intentado resolver el reto: hacer que la visión de objetos a través de lentes esféricos no perdiera nitidez.

Newton inventó un telescopio que solucionaba la llamada aberración cromática (que impide enfocar los colores en un solo punto), pero no la aberración esférica.

En el siglo pasado, en 1949, dos científicos plantearon el dilema en un artículo formal y a partir de allí, se conocería como el problema de Wasserman-Wolf. Pero hasta nadie había podido resolverlo plenamente.

Newton o Leibniz habían intentado resolver el reto: hacer que la visión de objetos a través de lentes esféricos no perdiera nitidez.

Una solución que otorga reconocimiento mundial

“Nos fue muy bien porque tuvimos la distinción del editor; eso es muy raro: menos del 1 por ciento de los 35 mil artículos que se han publicado en esa revista tienen esa distinción”, cuenta.

“Durante nuestro estudio, calculamos la eficiencia de 500 rayos, y el promedio de satisfacción de todos los ejemplos fue de 99.9999999999%.”.

El impacto de la investigación

Julio César Gutiérrez, profesor del Tec que asesora a Rafael en el doctorado, consideró que el haber resuelto el problema podrá implicar mejoras en el desarrollo de lentes.

“El diseño óptico tiene aplicaciones tecnológicas que involucran sistemas ópticos. Entonces los resultados tienen relevancia no solo teóricamente sino en otras aplicaciones.

Al respecto, en su publicación, los tres investigadores señalaron que la fórmula servirá para mejorar lentes, lentes de contacto, telescopios, binoculares y microscopios. 

Con información de Applied Optics, Phys.org y el Tec de Monterrey.